ЗОЛОТАЯ ПРОПОРЦИЯ, ЗОЛОТЫЕ КОНСТАНТЫ

Win-word.zip

ЗОЛОТАЯ ПРОПОРЦИЯ, ЗОЛОТЫЕ КОНСТАНТЫ

И ЗОЛОТЫЕ ТЕОРЕМЫ

Косинов Н.В.

Аннотация

Выявлен большой класс чисел, которые имеют свойства, присущие золотой пропорции (Ф=1,618…). Эти числа являются константами целочисленных последовательностей, члены которых заданы рекуррентными соотношениями a(n)=±ka(n–1)±a(n–2). Предельное значение отношений соседних членов в таких последовательностях порождает целое семейство золотых констант, имеющих свойства золотой пропорции. К выявленному классу последовательностей принадлежат последовательности Фибоначчи и Люка. У найденных новых последовательностей открыты такие же законы и свойства, какими обладают числа Фибоначчи и числа Люка.

1. Введение

Принято считать, что золотая пропорция (Ф=1,618) была известна еще Пифагору (VI в. до н. э.). Есть мнение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. Золотая пропорция присутствует в произведениях древнегреческих скульпторов. Обозначение “Ф” связано с именем Фидия – древнегреческого скульптора (5 в.до н.э.), в произведениях которого обнаружена золотая пропорция. Задача о золотом сечении пришла к нам из древних времен, - она описана в “Началах” Евклида. С золотой пропорцией связаны числа 1, 1, 2, 3, 5, 8, 13… , открытые в 13-м веке знаменитым итальянским математиком Фибоначчи. Отношение соседних чисел Фибоначчи по мере удаления от начала последовательности в пределе стремится к золотой пропорции. В эпоху Возрождения усиливается интерес к золотой пропорции среди ученых и художников. Лука Пачоли назвал ее “божественной” и посвятил золотой пропорции восторженную книгу “Божественная пропорция”. Считают, что прекрасные иллюстрации к книге были выполнены Леонардо да Винчи. В этой книге Лука Пачоли обожествил золотую пропорцию, сравнивал ее со Святой Троицей [4] и считал эту пропорцию “орудием мышления” и “принципом мира и природы”. Вслед за Пачоли великий астроном ХVI в. Иоганн Кеплер свое восхищение золотым сечением выразил в словах: “Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в крайнем и среднем отношении…Первое можно сравнить с ценностью золота, второе больше напоминает драгоценный камень”. Кеплер обратил внимание на проявление золотого сечения в растительном мире.

Французский математик Люка впервые назвал числовую последовательность1, 1, 2, 3, 5, 8, 13…числами Фибоначчи и открыл не менее фундаментальную последовательность 2, 1, 3, 4, 7, 11…, которая тоже связана с золотой пропорцией. Отношение соседних чисел Люка по мере удаления от начала последовательности в пределе стремится к золотой пропорции.

Последовательности чисел Фибоначчи F(n) = 1, 1, 2, 3, 5, 8, 13,… и чисел Люка: L(n)= 2, 1, 3, 4, 7, 11,… ученые все чаще встречают во многих явлениях окружающего мира. Это в значительной мере стимулирует интерес к золотой пропорции в настоящее время. В [3] установлено, что существует большой класс целочисленных последовательностей с однотипными свойствами, к которому принадлежат последовательности чисел Фибоначчи и Люка. Замечательной особенностью новых последовательностей является то, что константы целочисленных последовательностей этого класса обладают теми же свойствами, что и золотая пропорция. Для этого класса последовательностей справедлива обобщенная рекуррентная формула: a(n)=±ka(n–1)±a(n–2). Последовательности Фибоначчи и Люка представлены рекуррентной формулой a(n)=a(n–1)+a(n–2), которая является частным случаем рекуррентной формулы a(n)=ka(n–1)+a(n–2) при k =1.

С последовательностями Фибоначчи и Люка непосредственно связаны два числа: Ф=1,618… и φ=1/Ф=0,618... Они являются константами последовательностей Фибоначчи и Люка. Золотая пропорция (Ф=1,618) появляется как предел отношения соседних членов последовательности:

Золотое сечение (φ=0,618) появляется как предел отношения соседних членов последовательности:

Ниже представлены результаты исследований нового класса целочисленных последовательностей.

2. Константы целочисленных последовательностей и корни квадратных уравнений

Здесь мы приведем теоремы о том, что константы целочисленных последовательностей, члены которых определяются рекуррентными соотношениями a(n)=±ka(n–1) ±a(n–2), являются корнями квадратных уравнений вида: X²±kX±1=0.

ТЕОРЕМА 1: Константы целочисленных последовательностей, имеющих рекуррентные формулы вида: a(n)=±ka(n–1)+a(n–2), определяемые как предел отношения членов последовательности: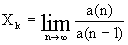

, являются корнями квадратных уравнений X²±kX–1=0.

ТЕОРЕМА 2: Константы целочисленных последовательностей, имеющих рекуррентные формулы вида: a(n)=±ka(n–1)–a(n–2), определяемые как предел отношения членов последовательности: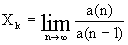

, являются корнями квадратных уравнений X²±kX+1=0.

3. 1-я золотая теорема и золотые константы

Хорошо известно, что золотая пропорция обладает замечательным свойством – обратная ей величина в точности равна числу, стоящему после запятой. Оказывается, что такая особенность не является привелегией одной золотой пропорции. Существуют и другие числа, обладающие таким же свойством. Например, таким же свойством обладают все числа, которые представляют собой золотую пропорцию в нечетной степени Ф^2m+1. В них обратная величина в точности равна числу, стоящему после запятой. Разность между золотой пропорцией в нечетной степени и обратной ей величиной равна целой части золотой пропорции в нечетной степени: Ф^2m+1 – Ф^-2m-1=“ЦЕЛАЯ ЧАСТЬ Ф^2m+1”. На этом не ограничивается семейство чисел, имеющих такое же свойство, как у золотой пропорции.

Чтобы продемонстрировать это приводим теорему для целочисленных последовательностей, члены которых заданы рекуррентными соотношениями a(n)=±ka(n–1)+a(n–2), которая утверждает, что константы таких последовательностей проявляют свойство золотой пропорции в нечетной степени Ф^2m+1.

1-я ЗОЛОТАЯ ТЕОРЕМА: Константы целочисленных последовательностей, имеющих рекуррентную формулу a(n)=±ka(n–1)+a(n–2), определяемые как предел отношения соседних членов последовательности:

проявляют свойство золотой пропорции в нечетной степени (Ф^2m+1) – их обратные значения равны разности между константой последовательности и числом k, которое является целой частью константы.

В соответствии с теоремой 1 для констант целочисленных последовательностей, члены которых заданы рекуррентными соотношениями a(n)=±ka(n–1)+(n–2), возможны два варианта квадратных уравнений, которые имеют вид:

X²–kX–1=0,

X²+kX–1=0.

Для последовательностей, члены которых заданы рекуррентным соотношением a(n)=ka(n–1)+a(n–2), общее уравнение: X_k–1/X_k=±k приводит к соотношению:

X–1/X=k

Отсюда следует: 1/X=X–k.

Число k является целой частью константы последовательности. Как видим, константы последовательностей обладают таким же свойством, как и золотая пропорция в нечетной степени – обратные значения констант в точности равны числам, стоящим у констант после запятой.

Для последовательностей, члены которых заданы рекуррентным соотношением a(n)=–ka(n–1)+a(n–2), общее уравнение: X_k–1/X_k=±k приводит к соотношению:

X–1/X=–k

Отсюда следует: 1/X=X– (–k)

Число –k является целой частью константы последовательности. Как видим, константы последовательностей, члены которых заданы рекуррентным соотношением a(n)=–ka(n–1)+a(n–2), обладают таким же свойством, как и золотая пропорция в нечетной степени. Обратные значения констант в точности равны числам, стоящим у них после запятой.

Эти числовые инварианты или константы целочисленных последовательностей, ввиду того, что они обладают свойствами золотой пропорции, названы золотыми константами [3]. Золотые константы характерны для класса числовых последовательностей, представленых обобщенной формулой a(n)=±ka(n-1)±a(n-2). К этому же классу последовательностей относятся числа Фибоначчи и числа Люка. Будем называть целочисленные последовательности с рекуррентными свойствами, представленными обобщенной формулой a(n)=±ka(n-1)±a(n-2), гармоническими последовательностями, поскольку их числовые инварианты обладают такими же свойствами, что и золотая пропорция, с которой тесно связано понятие гармонии в Природе.

Примеры целочисленных последовательностей, константы которых имеют свойства золотой пропорции, приведены в [3]. Здесь мы ограничимся примером новой последовательности, имеющей рекуррентную формулу a(n)=8a(n–1)+a(n–2). Эта рекуррентная формула при a(0)=2 и при a(1)=8 порождает последовательность вида: K₈(n) = 2, 8, 66, 536,… Это новая целочисленная последовательность. В энциклопедии Нейла Слоэна она зарегистрирована под номером A086594 [1,2,3].

Для этой последовательности золотая константа определяется в виде:

Число X₈=8,12310… переходит в обратное ему 1/X₈=0,12310…при вычитании целой части. Обратная величина числа X₈ в точности равна числу, стоящему после запятой. Таким же свойством обладает, как известно, золотая пропорция и все числа, полученные возведением золотой пропорции в нечетную степень Ф^2m+1. У последовательностей с рекуррентным свойством a(n)=8a(n–1)+a(n–2) с любыми начальными членами отношение соседних членов по мере удаления от начала стремится к золотой константе X₈=8,12310… Золотая константа этого семейства последовательностей является корнем уравнения вида: X₈–1/X₈=8.

Другими примерами чисел со свойствами, такими же, как у золотой пропорции, являются такие числа: X₁₀ =10,09901…, X₁₁=11,09016…, X₁₂=12,08276…и т. д. Они являются константами целочисленных последовательностей. Их обратные значения дают числа, стоящие после запятой: 1/X₁₀ = 0,09901…, 1/X₁₁= 0,09016…, 1/X₁₂ =0,08276…

Золотые константы и их обратные значения для последовательностей, члены которых заданы рекуррентными соотношениями a(n)=ka(n–1)+(n–2), приведены в табл.1.

Табл.1

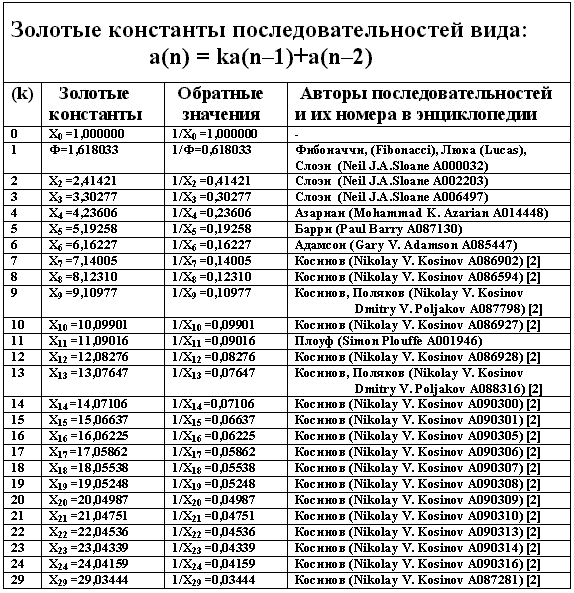
Как видим, существует большое количество чисел, обладающих свойствами золотой пропорции. Эти числа, как и сама золотая пропорция, являются константами целочисленных последовательностей с рекуррентным свойством a(n)=±ka(n-1)+a(n-2) или золотыми константами.

4. 2-я золотая теорема и золотые константы

Для целочисленных последовательностей, члены которых заданы рекуррентными соотношениями a(n)=±ka(n–1)–a(n–2), приводим теорему, которая утверждает, что константы таких последовательностей проявляют свойство золотой пропорции в четной степени Ф^2m.

Золотая пропорция, возведенная в квадрат обладает замечательным свойством – обратная ей величина в точности равна числу, дополняющему ее до ближайшего целого числа. Таким же свойством обладают числа, которые представляют собой золотую пропорцию в четной степени Ф^2m. Сумма золотой пропорции в четной степени и обратной ей величины равна ближайшему к ней целому числу:

Ф^2m + Ф^-2m= “БЛИЖАЙШЕЕ К Ф^2m ЦЕЛОЕ ЧИСЛО”.

Отсюда получим такую математическую формулировку этого замечательного свойства золотой пропорции в четной степени:

1/Ф^2m = “БЛИЖАЙШЕЕ К Ф^2m ЦЕЛОЕ ЧИСЛО” – Ф^2m.

2-я ЗОЛОТАЯ ТЕОРЕМА: Константы целочисленных последовательностей, имеющих рекуррентную формулу вида: a(n)=±ka(n–1)–a(n–2), определяемые как предел отношения членов последовательности: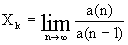

проявляют свойство золотой пропорции в четной степени (Ф^2m) – их обратные значения равны разности между числом k, которое является ближайшим к константе целым числом, и константой последовательности.

В соответствии с теоремой 2 для констант целочисленных последовательностей, члены которых заданы рекуррентными соотношениями a(n)=±ka(n–1)–(n–2), возможны два варианта квадратных уравнений, которые имеют вид:

X²–kX+1=0,

X²+kX+1=0,

Для последовательностей, члены которых заданы рекуррентным соотношением a(n)=ka(n–1) – a(n–2), общее уравнение: X_k+1/X_k=±k приводит к соотношению:

X+1/X=k

Отсюда следует:

1/X=k – X.

Число k является ближайшим к константе последовательности целым числом. Как видим, константы последовательностей обладают таким же свойством, что и золотая пропорция в четной степени – обратные значения констант в точности равны числу, дополняющему их до ближайшего целого числа.

X+1/X=–k

Отсюда следует:

1/X=– k–X.

Число –k является ближайшим к константе последовательности целым отрицательным числом. Как видим, константы последовательностей, члены которых заданы рекуррентным соотношением a(n)=–ka(n–1)–a(n–2), обладают таким же свойством, как и золотая пропорция в четной степени – их обратные значения в точности равны числу, дополняющему их до ближайшего целого числа.

Примеры целочисленных последовательностей, константы которых имеют свойства золотой пропорции в четной степени, приведены в [3]. Здесь мы ограничимся примером новой последовательности, имеющей рекуррентную формулу a(n)=10a(n–1)–a(n–2). Эта рекуррентная формула при a(0)=2 и при a(1)=10 порождает последовательность вида: K_8-(n) = 2, 10, 98, 970… Это новая целочисленная последовательность. В энциклопедии Нейла Слоэна она зарегистрирована под номером A087799 [1,2].

Для этой последовательности золотая константа определяется в виде:

Число X₈=9,89897…переходит в ближайшее целое число при добавлении к нему обратного значения 1/X₈=0,10102. Таким же свойством обладают все числа, образованные золотой пропорцией в четной степени Ф^2m. У последовательностей с рекуррентным свойством a(n)=10a(n–1)–a(n–2) с любыми начальными членами отношение соседних членов по мере удаления от начала стремится к золотой константеX₁₀=9,89897… Золотая константа этого семейства последовательностей является корнем уравнения вида: X₁₀+1/X₁₀=10.

Другими примерами чисел с такими же свойствами, как у золотой пропорции в четной степени, являются: X₈=7,87298…, X₁₁=10,9083…, X₁₂=11,9160…, и т. д. Эти числа являются константами целочисленных последовательностей. Их обратные значения являются дополнениями этих чисел до ближайшего целого числа: 1/X₈=0,12701…, 1/X₁₁=0,0916…, 1/X₁₂=0,0839…

Золотые константы и их обратные значения для последовательностей, члены которых заданы рекуррентными соотношениями a(n)=ka(n–1) – (n–2), приведены в табл.2.

Табл.2

Как видим, существует большое количество чисел, обладающих свойствами золотой пропорции в четной степени. Эти числа, как и сама золотая пропорция в четной степени, являются константами целочисленных последовательностей с рекуррентным свойством a(n)=±ka(n–1)–a(n–2) или золотыми константами.

5. Главные последовательности

Из теорем 1 и 2 следует, что золотые константы можно вычислить не только как предел отношения членов последовательности, но и как корни квадратных уравнений X²±kX±1=0.

Поэтому:

Формула для определения значений золотых констант при положительных k имеет вид: X=(k+sqrt(k^2±4))/2. Она непосредственно следует из уравнений: X²–kX±1=0. Формула для определения значений золотых констант для отрицательных k имеет вид: X=(–k–sqrt(k^2±4))/2. Она непосредственно следует из уравнений: X²+kX±1=0.

Каждая из рекуррентных формул a(n)=±ka(n–1)±a(n–2) при различных начальных числах порождает бесконечное количество целочисленных последоватенльностей, у которых будут одинаковые золотые константы. Однако, золотые константы по формулам: a(n) =((±k+sqrt(k^2±4))/2)^n+((±k–sqrt(k^2±4))/2)^n порождают только по одной последовательности в каждом семействе. У всех этих последовательностей начальными членами являются числа 2 и k. Эти последовательности будем называть главными последовательностями. Общая формула для определения членов главных последовательностей с помощью золотых констант, при положительных значениях k, имеет вид: a(n)=((k+sqrt(k^2±4))/2)^n+((k-sqrt(k^2±4))/2)^n [2]. Четные и нечетные члены главных последовательностей с рекуррентным свойством a(n)=ka(n–1)+a(n–2) вычисляются с помощью золотых констант по формулам [2]: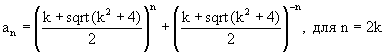

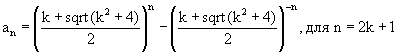
Любые произвольные члены главных последовательностей с рекуррентным свойством a(n)=ka(n–1)+a(n–2) вычисляются с помощью золотых констант и их обратных значений по следующей формуле [2]: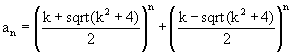

Для последовательностей с рекуррентным свойством a(n)=ka(n–1)–a(n–2) справедливо следующее соотношение:

Члены главных последовательностей с рекуррентным свойством a(n)=ka(n–1)–a(n–2) вычисляются с помощью золотых констант по следующим формулам [2]: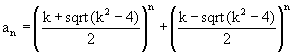

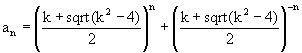
Для последовательностей из семейства a(n)=ka(n–1)+a(n–2) нулевой член главной последовательности: a(0)=((k+sqrt(k^2+4))/2)^0 + ((k-sqrt(k^2+4))/2)^0 = 2. Первый член главной последовательности: a(1)=((k+sqrt(k^2+4))/2)^1+((k-sqrt(k^2+4))/2)^1 = 2k/2=k и т.д.

Для последовательностей из семейства a(n)=ka(n–1)–a(n–2) нулевой член главной последовательности: a(0)=((k+sqrt(k^2–4))/2)^0+((k–sqrt(k^2–4))/2)^0=2. Первый член главной последовательности: a(1)=((k+sqrt(k^2–4))/2)^1+((k–sqrt(k^2–4))/2)^1=2k/2=k. Второй член главной последовательности: a(2)=((k+sqrt(k^2–4))/2)^2+((k–sqrt(k^2–4))/2)^2=k^2–2 и т.д.

Общая формула для определения членов главных последовательностей для отрицательных k имеет вид: a(n)=((–k–sqrt(k^2±4))/2)^n+((–k+sqrt(k^2±4))/2)^n.

Более подробные сведения о главных последовательностях можно найти в энциклопедии Нейла Слоэна [1,2] (A086902, A086903, A086594, A056918 , A087799, A086927, A057076, A001946, A087800, A086928, A078363 ).

6. Универсальные свойства золотых констант

Таким образом, выше было показано, что у всех последовательностей с рекуррентными формулами a(n)=±ka(n–1)±a(n–2) золотые константы проявляют такие же свойства, что и золотая пропорция. Ниже получим математическую формулу, которая будет единым образом выражать свойство всех золотых констант. Здесь приведена теорема, которая утверждает, что произведение золотых констант целочисленных последовательностей с рекуррентным свойством a(n)=±ka(n–1)±a(n–2) на абсолютную величину разности между золотой константой последовательности и числом k равно единице.

3-я ЗОЛОТАЯ ТЕОРЕМА: Произведение золотой константы целочисленной последовательности с рекуррентным свойством a(n)=±ka(n–1)±a(n–2), определяемой как предел отношения членов последовательности:

, на абсолютную величину разности между значением золотой константы и числом k равно единице: X(k–X)=±1.

Поскольку из 1-й золотой теоремы следует, что для последовательностей, члены которых заданы рекуррентным соотношением a(n)=±ka(n–1)+a(n–2), справедливы уравнения: 1/X=X–k и 1/X=X–(–k), а из 2-й золотой теоремы следует, что для последовательностей, члены которых заданы рекуррентным соотношением a(n)=±ka(n–1)–a(n–2), справедливы уравнения: 1/X=k–X , и 1/X=–k–X, то из всех этих уравнений непосредственно следует: X(k–X)=±1. Такое же соотношение справедливо для золотой пропорции: Ф(Ф – “ЦЕЛАЯ ЧАСТЬ Ф”) =1.

Таким образом, для всего класса последовательностей, члены которых заданы рекуррентными соотношениями a(n)=±ka(n–1)±a(n–2), в том числе и для последовательностей Фибоначчи и Люка, справедливо уравнение, которое связывает золотые константы X_k и коэффициенты k рекуррентных формул последовательностей в виде: X_k(k–X_k)=±1. Это общее свойство всех золотых констант, включая золотую пропорцию. Замечательная формула X_k(k–X_k)=±1 справедлива для любого целого k.

Ниже приведена теорема, которая утверждает, что сумма квадратов золотых констант двух целочисленных последовательностей, с симметричными рекуррентными формулами a(n)=±ka(n–1)+a(n–2) и a(n)=±ka(n–1)–a(n–2), при одинаковых значениях k, равна произведению числа k на сумму золотых констант: X₁²+X₂²= k(X₁+X₂) .

4-я ЗОЛОТАЯ ТЕОРЕМА: Сумма квадратов золотых констант двух целочисленных последовательностей, с симметричными рекуррентными формулами a(n)=±ka(n–1)+a(n–2) и a(n)=±ka(n–1)–a(n–2), при одинаковых значениях k, равна произведению числа k на сумму золотых констант.

Доказательство теоремы непосредственно следует из 3-й золотой теоремы. Поскольку X_k(k–X_k)=±1, то X₁(X₁–k)=X₂(k–X₂). Отсюда непосредственно следует: X₁² +X₂²=k(X₁+X₂).

7. Выводы

Целочисленные последовательности, для которых справедливо обобщенное рекуррентное соотношение a(n)=±ka(n–1)±a(n–2), представляют собой самостоятельный класс последовательностей, все константы которых проявляют свойства, присущие золотой пропорции (Ф=1,618) в четной или нечетной степени. К этому же классу последовательностей принадлежат последовательности чисел Фибоначчи и Люка. Предельные значения отношений соседних членов целочисленных последовательностей с рекуррентными свойствами a(n)=±ka(n–1)±a(n–2) порождают целый класс золотых констант, имеющих свойства золотой пропорции. Золотые константы последовательностей группируются в семейства, члены которых представлены степенными функциями главных инвариантов.

Приведенные теоремы 1 и 2 позволяют определить вид квадратных уравнений, корни которых совпадают с золотыми константами целочисленных последовательностей. В результате, точные значения золотых констант можно определить без вычисления удаленных от начала членов последовательности по рекуррентным формулам. В свою очередь, золотые константы позволяют легко определить любой член главных последовательностей по соответствующей алгебраической формуле. 1-я и 2-я золотые теоремы устанавливают свойства золотых констант, которые, как оказалось, соответствуют свойствам золотой пропорции. 3-я золотая теорема устанавливает универсальное свойство, присущее всем зототым константам целочисленных последовательностей с рекуррентными формулами a(n)=±ka(n–1)±a(n–2). Это свойство выражается формулой: (k–X_k)X_k=±1. Таким же замечательным свойством обладает золотая пропорция Ф(Ф-1)=1, а также все числа, представляющие собой золотую пропорцию возведенную в степень (Ф^m), при целочисленном показателе степени. 4-я золотая теорема устанавливает связь между зототыми константами последовательностей, имеющих симметричные рекуррентные формулы. Проведенные исследования позволили открыть новые целочисленные последовательности, константы которых обладают свойствами золотой пропорции. Новые последовательности внесены в энциклопедию Нейла Слоэна [1,2].

Источники информации

1. Neil J.A.Sloane http://www.research.att.com/~njas/sequences/

2. Nikolay V. Kosinov. Integer Sequences: A087204, A086902, A086903, A086594, A087798,

A087799, A086927, A087800, A086928, A088316, A090300, A090301, A090727,

A090305, A090306, A087215, A090307, A090308, A090728, A090309, A090729,

A090310, A090730, A090313, A090731, A090314, A090732, A090316,
A090733, A090247, A090248, A090249, A090251, A087281, A087265,
A087287, A065705, A087619, A089772, A089775, A088317, A088320.
3. Косинов Н.В. Золотые инварианты гармонических последовательностей.
http://kosinov.314159.ru/kosinov20.htm ,
4. Ковалев Ф.В. Золотое сечение в живописи: Учебное пособие. – К.: Выща шк., 1989.-143 с.

Демографические пенсии