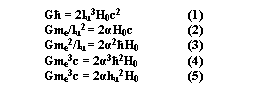
MDX – язык запросов к многомерным базам данных
Алгоритм «Вальс» - генератор самоподобных процессов
КАК ПОЛУЧИТЬ ТОЧНОЕ ЗНАЧЕНИЕ ГРАВИТАЦИОННОЙ КОНСТАНТЫ
G?Косинов Н.В.
E-mail:
kosinov@unitron.com.uaАннотация
Гравитационная константа G широко используется как в физических теориях, так и в практике. Однако по сравнению с другими константами ее значение определено с наименьшей точностью. Ученые считают, что трудности ее точного измерения связаны с тем, что на точность измерения влияют некоторые космические ритмы а также гравитационные волны, проходящие через Землю, вызывая квадрупольную деформацию Земли. В статье получено точное значение гравитационной константы G на основе установления ее связи с константами, которые относятся к электромагнетизму. Получены 25 эквивалентных соотношений для вычисления гравитационной постоянной G. Наиболее точное ее расчетное значение: G = 6,67286741(83)•10-11 m3 kg-1s-2. Предлагается при измерении константы G оценивать разность Gрасч. – Gизм. = ∆G. DeltaG является важной характеристикой как для изучения Земли, так и для изучения влияния космоса на Землю. Тогда различные значения G, полученные разными группами ученых, могут дать уникальную информацию о Земле и космосе.
Гравитационная константа
G широко используется как в физических теориях, так и в практике. Однако по сравнению с другими фундаментальными физическими константами ее значение определено с наименьшей точностью. Некоторые ученые считают, что именно неточность определения гравитационной постоянной является причиной многих неудач во время запусков космических ракет и искусственных спутников Земли. Неточность гравитационной постоянной, заложенная при расчетах траекторий космических ракет, искусственных спутников Земли и межпланетных космических кораблей стала основной причиной их сходов со своих орбит, “уходов” в открытый космос или сгорания в плотных слоях атмосферы [1].Значение
G было определено впервые английским физиком Г.Кавендишем в 1798 г. на крутильных весах путем измерения силы притяжения между двумя шарами. Им было получено следующее значение константы: G=6,740(50)• 10-11 m3kg-1s-2. В последующие годы измерения гравитационной константы продолжались. В 1982 году G.Luther и W.Towler получили значение [3]: G=6,67260(50)• 10-11 m3kg-1s-2. В 1986 году комиссией по фундаментальным физическим константам CODATA было рекомендованно новое значение гравитационной константы: G = 6,67259 (85)• 10-11 m3kg-1s-2. Результаты измерений гравитационной константы, полученные разными группами ученых, имеют большие расхождения. В 1998 году комиссией по фундаментальным физическим константам CODATA рекомендованно значение гравитационной константы, которое по точности значительно уступает предыдущему значению: G=6,673(10)• 10-11 m3kg-1s-2 [2]:В 2000 году группе из Университета Вашингтона в Сиэтле удалось получить получить результат
G=6,67390 • 10-11 m3kg-1s-2 с погрешностью 0,0014% [9]. Два наиболее точных измерения G были получены группами ученых в Сиэтле и Международном бюро мер и весов под Парижем, причем в обоих случаях ошибки эксперимента составляли около 1/10000, однако разница полученных значений превышает возможные погрешности почти в 10 раз [1]. На точность измерения константы G оказывают влияние множество факторов. В частности, на ее точность влияют некоторые космические ритмы (солнечные, лунные, звездные), которые пока не нашли объяснения [3].Как отмечает Э.Халилов [1], причиной всему являются гравитационные волны, пронизывающие все космическое пространство и проходящие через Землю, вызывая квадрупольную деформацию как самой Земли, так и околоземного пространства. Ученый установил, что через Землю проходят сверхдлинные гравитационные волны как минимум трех порядков с периодами 2,5 года, 7,7 лет и 40-60 лет, наложенные друг на друга и влияющие на взаимное притяжение грузиков в весах Кавендиша
, причем по - разному, в зависимости от географического положения измерительных лабораторий и времени измерений. По мнению Э.Халилова, ученым не удастся зафиксировать одновременно в разных точках земного шара одно и то же значение гравитационной постоянной, за исключением единственного случая, когда гравитационная волна будет проходить через Землю в точке смены полупериодов. Именно в этот момент тензор напряжений, вызываемых прохождением гравитационной волны через Землю будет равен нулю.Если учесть, что сквозь Землю проходят волны с различными периодами, то условие для нулевого значения тензора напряжений может выполняться один раз в несколько сотен лет, что делает практически нереальным получение точного значения
G с помощью измерений. В этом клубке проблем уточнение значения гравитационной константы приобретает особую актуальность. Сложность экспериментальных работ по измерению гравитационной константы G заставляет искать другие способы определения ее точного значения. По моему мнению, единственно точное значение гравитационной константы G можно получить, если удастся установить ее связь с фундаментальными физическими константами.Большинство физических констант не поддаются прямому измерению, поэтому их значения определяют косвенно из соотношений, связывающих их с другими константами. Здесь решающим фактором является то, что большинство констант связаны законами физики с другими константами. На этом основаны способы определения значений констант. Однако в отношении гравитационной константы
G считается, что она не связана ни с какими фундаментальными физическими константами.В работах [4,5,7,8] выявлена взаимосвязь, существующая между константами. В частности, получены следующие космологические уравнения [5]:
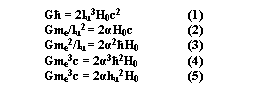
Соотношения, очень близкие к формулам (3) и (4), были получены в 1931 году Стюартом [10]. Уравнения (1) - (5) отражают связь фундаментальных физических и космологических констант. Возможно, что за этими уравнениями стоит какой-то физический закон, устанавливающий связь между гравитацией и электромагнетизмом.
Космологические уравнения напрямую выводят на связь двух важнейших констант
G и H0. Удалось получить несколько эквивалентных соотношений, связывающих постоянную Хаббла H0 и гравитационную константу G. В связи с тем, что отношение G/H0 определяется исключительно посредством высокоточных констант микрофизики, то его значение оказалось беспрецедентно точным - на несколько порядков точнее значений самих констант G и H0.В таблице 1, в качестве примера, приведены 10 эквивалентных формул для вычисления отношения
G/H0 с помощью констант электромагнетизма и значения, полученные по этим формулам.Табл.1
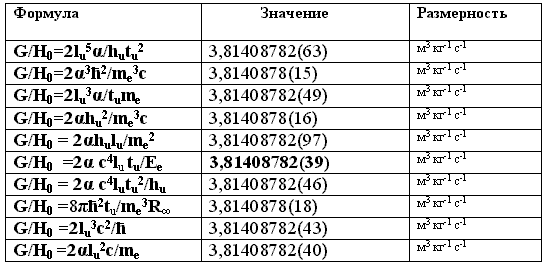
Обнаружены и другие комбинации космологических констант, которые выражаются с помощью констант электромагнетизма. Так, например, масса Метагалактики
MU совместно с константами G, H0 ,RMG дает интересные комбинации, которые выражаются исключительно фундаментальными физическими константами (табл.2) [5]:Табл.2
Выявленная взаимосвязь космологических и микрофизических констант является подтверждением концепции единства мира. Взаимосвязь констант
G и H0, представленная константами, относящимися к микромиру, указывает на то, что существует еще не открытый физический закон, который должен отражать связь между электромагнетизмом, гравитацией и характеристиками раздувающейся Вселенной.В [4,5,8] выявлена связь гравитационной постоянной с фундаментальными физическими константами и получены следующие формулы для вычисления значения константы
G: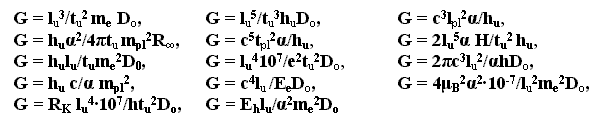
Из приведенных формул видно, что константа
G выражается с помощью других фундаментальных констант очень компактными и простыми соотношениями. В число констант, с помощью которых представлена гравитационная константа, входят такие константы: квант hu, скорость света c, постоянная тонкой структуры α, постоянная Планка h, число π, константы пространства-времени (lu,tu), элементарная масса me, элементарный заряд e, большое число Do, планковские единицы длины lpl, массы mpl, времени tpl, магнетон Бора μB, постоянная Хаббла H0 , константа Ридберга R∞, энергия покоя электрона Ee, константа фон Клитцинга RK, энергия Хартри Eh.Большое число
Do, входящее в соотношения, определяется из фрактала протона [6] (рис.1), откуда проистекает следующая фрактальная формула:![]()
Здесь:
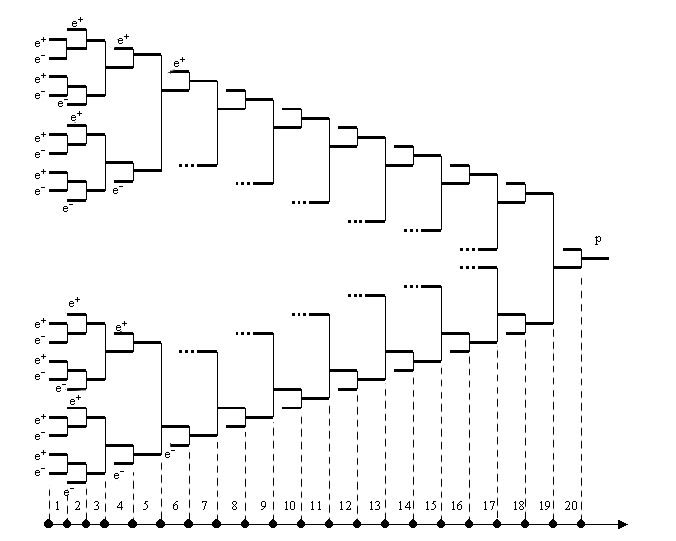
Рис.1. Фрактал протона.
Наиболее точное значение большого числа
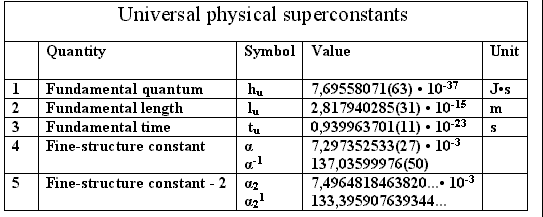
Do = 4,16650385(15)∙1042. В формулы также входят константы hu , lu, tu из группы универсальных суперконстант (табл.3), которые являются первичными и независимыми константами [7,8]:Табл.3
Ниже приведены 25 эквивалентных формул для вычисления гравитационной константы
G.Все 25 формул дают практически одинаковые значения гравитационной постоянной. Различия очень незначительные и наблюдаются в седьмом-девятом знаках, что связано с различной точностью тех констант, посредством которых представлена гравитационная константа
G: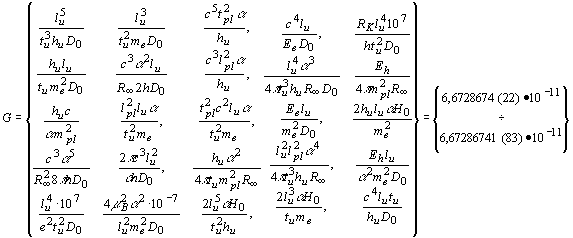
В таблице 4 приведены экспериментальные значения, полученные в период 1798 - 1998 г.г. [3] и наиболее точные расчетные значения константы
G, полученные по приведенным выше формулам [5]:Табл.4
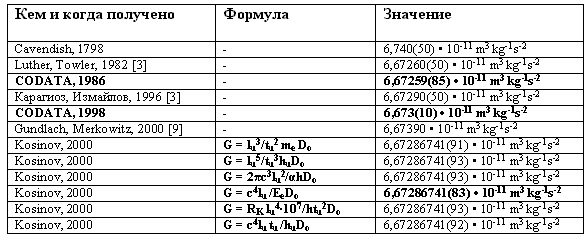
Вышеизложенное позволяет по-новому подходить к оценке результатов всех ранее проведенных экспериментов по определению значения константы
G. Различные значения G, полученные разными группами ученых, могут оказаться весьма информативными совершенно в ином аспекте. Предлагается при измерении константы G оценивать разность Gрасч. – Gизм. = ∆G. Если использовать разность Gрасч. – Gизм.=∆G, то эта величина может выступать в новом качестве. Она является важной характеристикой как для изучения Земли, так и для изучения влияния космоса на Землю. В этом случае, измерения значения гравитационной константы, проведенные в разных точках земного шара в одно и тоже время, в совокупности могут дать уникальную информацию о Земле и космосе. В этой связи становится целесообразным создание специальной сети измерительных лабораторий, оснащенных однотипным оборудованием, которые должны быть расположены в различных точках земного шара. Задачей этих лабораторий должно быть точное определение значения разности ∆G.ВЫВОДЫ
ЛИТЕРАТУРА
